
Teste à proporção
Em sondagens e votações é habitual prever que uma votação será determinada em função de uma amostragem.
Pelo teorema do limite central qualquer distribuição pode ser considerada aproximadamente normal quando tiver mais de 30 observações.
No caso da aproximação de uma variável binomial a uma variável normal tem-se que se pode fazer desde np>5 e n(1-p)>5 pelo que nalguns casos a partir de 10 observações é possível fazer esta aproximação.
O desvio padrão será dado por:
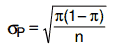
E o teste será dado por:
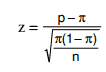
Por exemplo, uma sondagem de ciclistas aponta:
150 são contra a obrigatoriedade do capacete
50 são a favor
A probabilidade de ser contra é 0,75.
O desvio padrão será 1,7 /4 / 14,1= 0,03
O intervalo de confiança a 95% deste valor corresponde a um Z de 1,96 e é aproximandamente entre 0,69 e 0,81.
Isto significa que o valor verdadeiro da proporção na população poderia ser diferente dos 0,75 mas que estaria dentro deste intervalo de 0,69 a 0,81.
Uma hipótese de que a maioria dos ciclistas é a favor teria um valor z de -8,33.
Habitualmente para valores de Z abaixo de -3,4 considera-se que a probabilidade é praticamente nula pelo que seria praticamente zero.
