
Exercícios
1) Alguns alunos de uma determinada escola praticam uma ou mais de 3 modalidades desportivas,nomeadamente, futebol, basquetebol e andebol. São conhecidas as seguintes proporções:
- 30% praticam futebol;
- 20% praticam basquetebol;
- 20% praticam andebol;
- 5% praticam futebol e basquetebol;
- 10% praticam futebol e andebol;
- 5% praticam basquetebol e andebol;
- 2% praticam todas estas modalidades.

a) se escolhermos um aluno ao acaso, qual a probabilidade de ser:
i. um jogador de futebol ou de andebol?
P(fut)+P(and)-P(fut e and)= 30 + 20 – 10 = 40
ii. apenas jogador de futebol?
P(fut)+P(fut e bas)-P(fut e and)+P(fut e and e bas)= 30 – 10 – 5 + 2 = 17
iii. um atleta?
P(fut)+P(and)-P(fut e and)+P(só basq)=40+12=52
b) Se escolhermos um aluno atleta, qual a probabilidade de ser:
i. apenas jogador de futebol?
ii. um jogador de futebol ou de andebol?
2) Num determinado aquário encontram-se 4 peixes dourados e 6 vermelhos para venda. O Sr. Zé vai comprar 2 desses peixes, não tendo preferência pela cor. Assim, selecciona-se aleatoriamente um conjunto de 2 peixes.
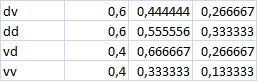
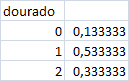
a) Qual a distribuição da v.a. X que representa o número de peixes dourados que calham a este cliente?

| Peixes | |
|---|---|
| 0 | 2 vermelhos |
| 1 | vermelho-dourado ou dourado-vermelho |
| 2 | dourado-dourado |
b)Chegado a casa, os 2 filhos do Sr. Zé começam a discutir quem escolhe primeiro o seu peixinho, antes mesmo de os verem. Decidem pois que, se pelo menos 1 dos peixes for dourado, o filho mais velho pode escolher primeiro. Caso contrário, escolhe primeiro o filho mais novo. Represente Y a v.a. que indica se foi o filho mais velho a escolher (Y = 1) ou não (Y = 0). Determine a função de probabilidade de Y. Identifique esta distribuição.
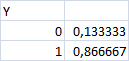
É uma distribuição discreta e dictómica que só toma 2 valores e está directamente dependente do valor anterior.
c) As v.a.’s X e Y são independentes? Justifique adequadamente.
Não são independentes dados que o valor de Y depende do valor de X.
3) Um foguete espacial é constituído por 3 partes distintas, cápsula, corpo e depósitos. Representem as v.a.’s X, Y e W como sendo o peso da cápsula, o peso do corpo do foguete e o peso dos depósitos, respectivamente, em toneladas. Sabe-se que X~N(5;1), Y~N(10;2) e X~N(7,2) , e sendo as três variáveis independentes entre si.

a) Qual a probabilidade de o peso da cápsula estar compreendido entre 1,5 vezes e 3 vezes o peso do corpo?
O valor esperado da soma de 3 variáveis corresponde à soma dos valores esperados de cada variável.
E[A+B+C]= E[A]+E[B]+E[C]= 5+10+7=22
Da mesma forma a variância da soma é igual à soma das variâncias.
VAR[A+B+C]= VAR[A]+VAR[B]+VAR[C]=1*1+2*2+2*2=9
10*1,5 = 15
10*3=30
E possível aproximar a nossa nova distribuição N(22,3) ~N(0,1) através das transformações.
O gráfico foi criado em R usando os comandos:
mean=22; sd=3; lb=15; ub=30;
x <- seq(-4,4,length=100)*sd + mean
hx <- dnorm(x,mean,sd)
plot(x, hx, type=”n”, xlab=”Peso”, ylab=”Densidade”,
main=”Distribuição Normal”, axes=FALSE)
i <- x >= lb & x <= ub
lines(x, hx)
polygon(c(lb,x[i],ub), c(0,hx[i],0), col=”red”)
area <- pnorm(ub, mean, sd) – pnorm(lb, mean, sd)
result <- paste(“P(“,lb,”< IQ <“,ub,”) =”, signif(area, digits=3))
mtext(result,2)
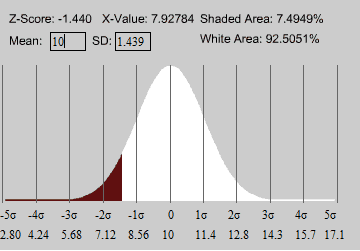
b) Qual o peso h que o corpo do foguete ultrapassa em 92.5% das vezes?
Aqui aplica-se o raciocínio inverso. Parte-se do valor da probabilidade para determinar o valor do Z e depois do x.
[math]\Phi(z)=0,925 => Z = 1,439531[/math]
Como é o valor que e ultrapassado em 92,5% dos vezes iremos determinar o valor acima do qual tal se verifica.
[math]z=\frac{x-\overline{x}}{\sigma}=\frac{x-10}{\sqrt{2}}= 1,439531[/math]
Como a distribuição normal é simétrica podemos fazer esta operação.
[math]x=10-1,439531×2=7,12[/math]
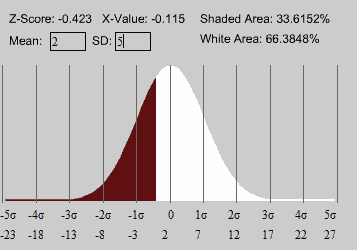
c) Qual a probabilidade de o peso da cápsula mais o peso dos depósitos excederem o peso do corpo do foguete?
N(2; 5)= N(5+7-10;5)
Fazendo a soma das distribuiçoes temos que em média o peso será superior em 2 kilos. pelo que se quer determinar quando o peso é maior que zero.
[math]z=\frac{x-\overline{x}}{\sigma}=\frac{0-2}{5}=-0,4[/math]
[math]\Phi(z)=0,344578[/math]
Probabilidade = 0,633
4) O tempo de espera (em minutos) por um autocarro é uma v.a. T com a seguinte função densidade de densidade de probabilidade:
| Função Densidade | Intervalo de Tempo |
|---|---|
| 1/2 | 0 |
| 1/4 | 1 |
| 0 | 0 |
a) Determine a função de distribuição da v.a. T (Sugestão: esboce primeiro o gráfico de f(t)).
x/2 0<t<1
1/2+(x-1)/4 1<t<3
b) Determine o tempo médio e o tempo mediano de espera pelo autocarro.
tempo médio = 1/2 * 0,5 + 2 * 0,5 = 1,25
mediano = 1
c) Qual é a probabilidade de esperar menos de 1 minuto pelo autocarro, sabendo que já estou à espera há 0.5 minuto?
P(a|b) = P(a) / P(b)
P(menos de 1)=0.5
P(menos de 0,5)= 0,25
P(b)=1-0,25=0,75
0,25/0,75= 1/3=0,33
d) Durante o ano tenho de apanhar este autocarro 100 vezes. Qual é o número médio de vezes, nesse ano, em que espero menos de meio minuto?
np = 100 * 0,25 = 25
http://bioinforx.com/free/bxarrays/venndiagram.php
Usando um modelo de regressão linear da satiçao com as 7 variáveis tem-se:
lm(formula = csatisf ~ flexib + imagfor + imagvend + preco +prodqual + rapid + relacao, data = Dataset)
Residuals:
Min 1Q Median 3Q Max
-0.93928 -0.16103 0.05892 0.23233 0.71929
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.56711 0.44521 -1.274 0.2059
flexib 0.28995 0.03679 7.882 6.34e-12 ***
imagfor 0.42850 0.05965 7.183 1.73e-10 ***
imagvend -0.19619 0.08473 -2.315 0.0228 *
preco 0.17611 0.18698 0.942 0.3487
prodqual -0.04598 0.03180 -1.446 0.1516
rapid 0.24000 0.18005 1.333 0.1858
relacao 0.13164 0.35051 0.376 0.7081
Isto aponta que apenas 3 factores estão fortemente relacionados com o nível de satisfação dos clientea flexibilidadem a imagem da formação e das vendas.
