
Exercício Poisson
O nº médio de aviões que aterram num determinado aeroporto é de 3 em cada 2 minutos. Sabe-se que o nº de aviões que aterram no aeroporto é bem modelado por uma distribuição de Poisson.
a) Calcule a probabilidade de num período de 2 minutos aterrarem no máximo 2 aviões.
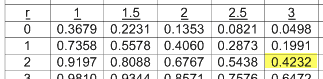
Dado a média serem 3 a probabilidade acumulada é 0.4232
b) Calcule a probabilidade de num período de 6 minutos não aterrar qualquer avião.
O período de 6 minutos é 3x o período de 2 minutos pelo que o valor esperado é 3×3 = 9
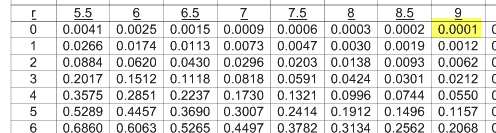
Novamente da tabela pode-se ver que o valor esperado de ocorrências é de 0.0001
Esta tabela de Poisson vem de
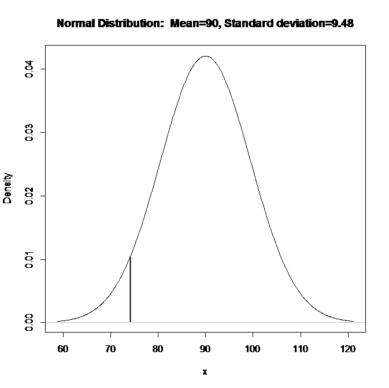
c) Qual a probabilidade aproximada de que numa hora, seleccionada ao acaso, ocorram pelo menos 75 aterragens?
Neste caso terá que ser feita uma aproximação da Poisson à normal.
uma hora = 60 minutos = 30 * 2 minutos
Ou seja o valor esperado será de 3 *30 = 90 aterragens.
Na aproximação da Poisson à normal temos que a média é igual
e o desvio padrão é a raiz da média = 9.48
Calculando o Z tem-se Z= (74,5-90)/9.48=-1.6338
>pnorm(74.5,mean=90,sd=sqrt(90),lower.tail=FALSE) [1] 0.9488541
Logo a hipótese de ter pelo menos 75 aterragens é 0,9488541.
Agradeço o comentário feito a esta resolução que permitiu melhorar a qualidade da explicação.
