
Distribuição normal
A distribuição normal tem uma função densidade de probabilidade complexa pelo que habitualmente se recorre a tabelas, calculadoras ou computadores para calcular a mesma.
Propriedades
A distribuição normal tem uma média e um desvio padrão associado sendo os seus valores tabelados no caso de uma distribuição com média 0 e desvio padrão 1.
Como saber o valor
Pode-se conhecer o valor do Z e querer-se determinar o valor da probabilidade acumulada até ao ponto ou pode-se saber o valor da probabilidade que se pretende e querer obter o valor do Z.
A tabela
A tabela de distribuição normal só apresenta valores de Z positivos e a probabilidade acumulada para Z=0 é de 0,5.
Isto acontece porque a distribuição normal é simétrica.
Valores extremos
No caso de valores acima de 3,9 considera-se que o valor é praticamente 1 pelo que não esta tabelado.
Tabela de distribuição normal
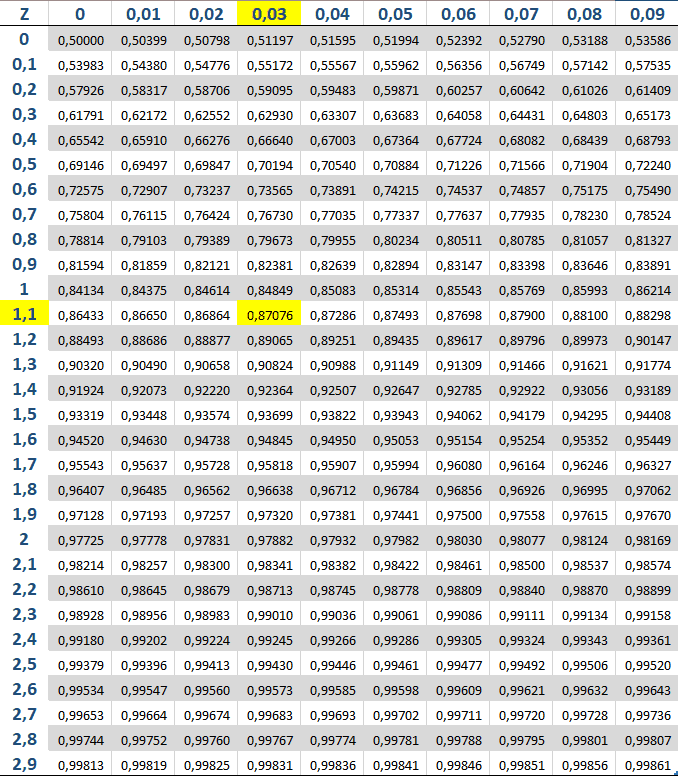
Como usar a tabela
Exemplo
Na tabela está marcado a amarelo como descobrir o valor de Z de 1,13 o valor da probabilidade acumulada da distribuição normal é de 0,87076
Procura-se as décimas na coluna da esquerda (1,1) e as centésimas na linha de cima da tabela (0,03).
Representação
É habitual representar o valor lido a partir da tabela da probablidade acumulada como sendo
Cálculo do complementar
Para calcular o valor complementar pode-se usar:
Outras tabelas
Por vezes existem tabelas de distribuição normal que mostram só a probabilidade de estar entre zero e o valor de Z pelo que os resultados são necessariamente diferentes e inferiores a 0,5.
Distribuição normal em programas
Excel
Em Excel a função
Norm.dist(x; média; desvio padrão; acumulado)
devolve o valor da probabilidade acumulada da distribuição normal directamente sem ter que calcular o valor do Z antes.
R
Em R pode-se usar a função
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
Em R até se pode criar gráficos como o do lado só com um comando.
local({
.x <- seq(-3.291, 3.291, length.out=1000)
plotDistr(.x, dnorm(.x, mean=0, sd=1), cdf=FALSE, xlab="x",
ylab="Density",
main=paste("Normal Distribution: Mean=0, Standard deviation=1"),
regions=list(c(-5, 1.13)), col=c('#00FFFF', '#BEBEBE'),
legend.pos='topright')
})
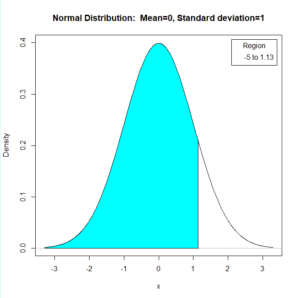
A área a azul corresponde a 87% da área debaixo da linha da distribuição normal sendo assim a probabilidade acumulada com um valor de Z de 1,13
Teste unilateral ou bilateral
Nível de significância
No caso de lhe ser dado um nível de significância pretendido terá que ver se é para ambos os lados ou só para um.
No caso de ser um teste de igualdade será para ambos os lados.
Por exemplo, entre Z=-1,96 e Z=196 tem 95% da área enquanto se quiser só para um dos lados ficará que com Z menor que 1,645 tem a mesma área de 95%.
Teste bilateral
Se tiver a ver qual é a cadeira que é confortável terá que será adequadas para pessoas com mais que uma certa altura mas menos que outra.
Este tipo de teste é bilateral.
Teste unilateral
Se tiver uma porta só lhe interessa ver a partir de que altura não passam as pessoas.
As crianças por mais pequenas que sejam podem sempre passar em qualquer porta.
Este tipo de teste é unilateral.
